【题目描述】：
    T国有N个城市，用若干双向道路连接。一对城市之间至多存在一条道路。
    在一次洪水之后，一些道路受损无法通行。虽然已经有人开始调查道路的损毁情况，但直到现在几乎没有消息传回。
    幸运的是，此前T国政府调查过每条道路的强度，现在他们希望只利用这些信息估计灾情。具体地，给定每条道路在洪水后仍能通行的概率，请计算仍能通行的道路恰有N-1条，且能联通所有城市的概率。
【题目解法】：
    我们考虑类比无向图的最小生成树算法，得到它的扩展：
    1.令g[i][j]表示(i,j)边的权值
    2.令g[i][i]=-sigma(g[i][j]) i!=j
    那么n-1阶主子式的相反数就是：每个生成树边权乘积之和

    但是这题如果直接这样做的话不能保证其他的边不再树上
    因此我们需要对每一种方案乘上其他边不在树上的概率
    也就是(引用自zky's blog)：

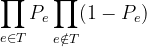
    然后我们可以令原来的边权p[i][j]=p[i][j]/(1-p[i][j])
    最后答案再乘上所有(1-p[e])的乘积（注意双向边只能乘一次）
    证明的话：
    1.如果一个边e被选了，显然他对答案的贡献为p[e]/(1-p[e])*(1-p[e])=p[e]
    2.如果e不被选，那么它对答案的贡献就是(1-p[e])
    细节的话：如果一个1-p[e]等于0，把它当成eps计算即可

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=55;
const double zero=1e-8;
int n; double a[N][N],ans,Ans;
inline long long getint()
{
    long long x=0; char c=getchar(); bool flag=false;
    while ((c!='-')&&((c<'0')||(c>'9'))) c=getchar();
    if (c=='-') flag=true,c=getchar();
    while ((c>='0')&&(c<='9')) x=x*10+(long long)(c-'0'),c=getchar();
    if (flag) return -x; else return x;
}
double calc(double x) {return max(x,zero);}
void init()
{
    n=getint(); Ans=1;
    for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) {scanf("%lf",&a[i][j]); if (i<j) Ans*=calc(1-a[i][j]);}
    for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) a[i][j]=a[i][j]/calc(1-a[i][j]);
    for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) if (i!=j) a[i][i]-=a[i][j];
    for (int i=1; i<=n; i++) for (int j=1; j<=n; j++) a[i][j]=-a[i][j];
}
void solve()
{
    ans=1; n--;
    for (int i=1; i<=n; i++)
    {
        for (int j=i; j<=n; j++)
        {
            if (fabs(a[j][i])<zero) continue; if (i!=j) ans=-ans;
            for (int k=1; k<=n; k++) swap(a[i][k],a[j][k]); break;
        }
        if (fabs(a[i][i])<zero) continue; ans=ans*a[i][i];
        for (int j=i+1; j<=n; j++)
        {
            double tmp=a[j][i]/a[i][i];
            for (int k=1; k<=n; k++) a[j][k]-=tmp*a[i][k];
        }
    }
    ans=ans*Ans;
    printf("%.10lf\n",ans);
}
int main()
{
    init();
    solve();
    return 0;
}